Poster #215, Ground Motions
Near-fault large-event ground motion models
Poster Image:
Poster Presentation
2020 SCEC Annual Meeting, Poster #215, SCEC Contribution #10237 VIEW PDF
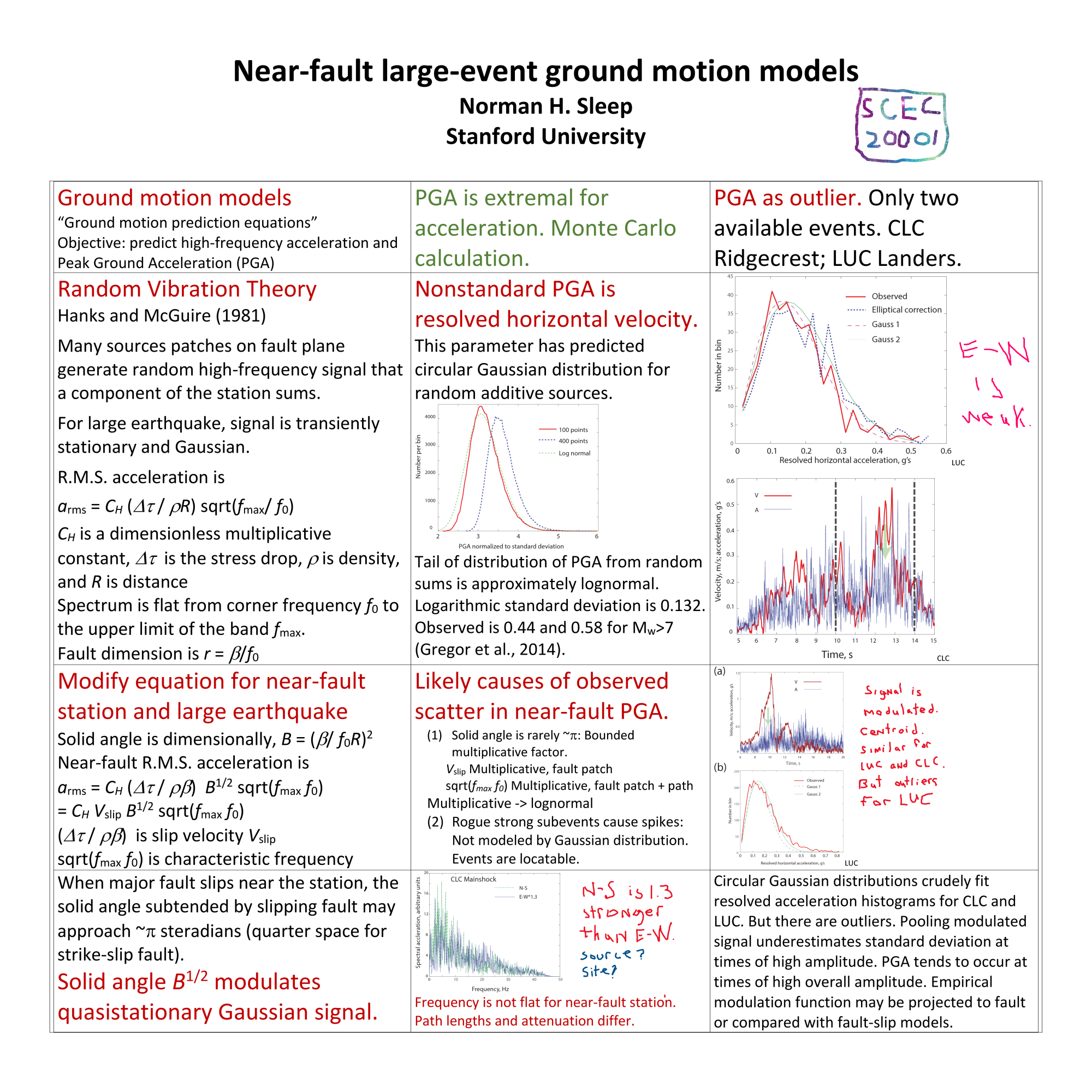
o reach the station from the fault. Additive Gaussian statistics of many zero-mean terms then apply for the high-frequency signal. Predicted accelerations for one horizontal component have Gaussian distributed about zero and scale with a low-frequency modulation function M that is proportional to the square root of B. The resolved horizontal acceleration has a circular Gaussian distribution. There are two relevant records: station CLC recorded strong shaking from the 2019 Ridgecrest mainshock ~3 km from the fault and station LUC ~1.25 km from the fault of the 1992 Landers. The resolved horizontal accelerations at during strong shaking are crudely fit by circular Gaussian distributions. The central limit theorem predicts such convergence near the centroid of the distribution. But there are strong outliers. I define peak ground acceleration (PGA) in the nonstandard manner as the peak outlier of resolved horizontal acceleration for statistical tractability. Then vagaries associated with circular Gaussian distributions at given B cause only slight scatter in PGA. The logarithmic standard deviation is only 0.132 compared with published values of 0.44 to 0.58 for PGA. Physically, rogue subevents violate the standard statistical assumption that no one small source contributed disproportionately to the sum. Such subevents may be located with multiple stations. Alternatively, the modulation function varied as slip on large domains on the fault plane waxed and waned. The modulation function is crudely the square-root of the angle subtended by slipping fault that can be inferred from models of low-frequency slip. The predictions of my model are then similar to those of a low-frequency dynamic model where stochastic high frequency moment release is added to the sliding fault plane.
SHOW MORE
SHOW MORE
















































